Singleton (mathematics)
In mathematics, a singleton, also known as a unit set,[1] is a set with exactly one element. For example, the set {0} is a singleton.
The term is also used for a 1-tuple (a sequence with one element).
Contents |
Properties
Note that a set such as {{1, 2, 3}} is also a singleton: the only element is a set (which itself is however not a singleton). A singleton is distinct from the element it contains,[1] thus 1 and {1} are not the same thing.
A set is a singleton if and only if its cardinality is 1. In the set-theoretic construction of the natural numbers, the number 1 is defined as the singleton {0}.
In axiomatic set theory, the existence of singletons is a consequence of the axiom of pairing: for any set A that axiom applied to A and A asserts the existence of {A,A}, which is the same as the singleton {A} (since it contains A, and no other set, as element).
If A is any set and S is any singleton, then there exists precisely one function from A to S, the function sending every element of A to the one element of S.
Applications
In topology, a space is a T1 space if and only if every singleton is closed.
Structures built on singletons often serve as terminal objects or zero objects of various categories:
- The statement above shows that the singleton sets are precisely the terminal objects in the category Set of sets. No other sets are terminal.
- Any singleton can be turned into a topological space in just one way (all subsets are open). These singleton topological spaces are terminal objects in the category of topological spaces and continuous functions. No other spaces are terminal in that category.
- Any singleton can be turned into a group in just one way (the unique element serving as identity element). These singleton groups are zero objects in the category of groups and group homomorphisms. No other groups are terminal in that category.
Definition by indicator functions
Let  be a class defined by an indicator function
be a class defined by an indicator function
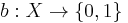 .
.
Then  is called a singleton if and only if, for all x ∈ X,
is called a singleton if and only if, for all x ∈ X,
for some y ∈ X.
Traditionally, this definition was introduced by Whitehead and Russell[2] along with the definition of the natural number 1, as
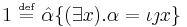 , where
, where 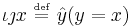 .
.
See also
References
- ^ a b
Stoll, Robert (1961). Sets, Logic and Axiomatic Theories. W. H. Freeman and Company. pp. 5–6.
- ^ Whitehead, Alfred North; Bertrand Russell (1910). Principia Mathematica. p. 37.